이전 글에서 말했 듯이 계산 범위를 넘어갔을 때 else로 처리한다고 했던 것에 대한 내용이다.
내가 생각해본 이론 설명
자세하게 말한다면 IK를 구현할려면 a, b, c가 필요하다.
a가 첫번째 팔 길이, b가 두번째 팔 길이이고 c가 a와 b의 삼각형에서 빗변이다.
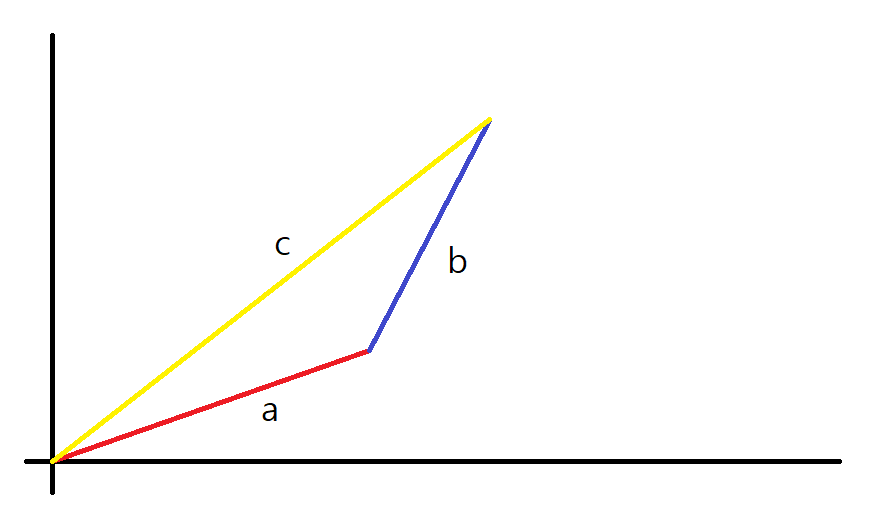
사진으로 보면 이렇다.
근데.. 여기에서 마우스 포인터의 x, y와 센터점까지 길이가 c가 될 수 있는데 a와 b가 정해져 있으므로 c가 a + b를 벗어나면 삼각함수에서 계산이 전혀 되지가 않는다. 아마 코딩하면 nan(ind)인가 이걸로 값이 뜰 것이다..
그래서 이 경우 내가 생각한 해결 방법으론 c가 a + b를 넘어갔을 때 그냥 a와 b를 쫙 펼치고 삼각함수로 하든 어떻게든 해서 마우스쪽의 방향으로 IK를 돌려버리는 것을 생각했다..
그래서 일단 다시 샤프를 잡고 쫙 펴졌을 때를 그린 후에 삼각형을 찾아봤다.
그러더니.. 한가지 나왔다..

일단 빨간색 점의 경우 마우스 포인터의 위치이다.
그래서 마우스 포인터의 위치로 직각삼각형을 그릴 수 있다..! 이걸 이용하면 밑변과 높이인 x, y를 구할 수 있다는 것..!
어쨋든 이전 글에서 θ1을 구할 때
float theta1 = atan2(mouse_y, mouse_x) - atan2(b * sin(theta2), a + b * cos(theta2));이런 공식을 썼다. 근데 이 공식이 θ1 + B에서 B인 atan2(b * sin(theta2), a + b * cos(theta2)) 이걸 그냥 뺀거다.
그렇기 때문에 θ1 + B가 필요한 각도이다..!
그래서 그냥 theta1 = atan2(mouse_y, mouse_x)를 가져다 썼다.
그럼 이걸로 θ1을 구했기 때문에 이걸로 밑변과 높이를 구할 수 있게 된다.
근데 여기에서 필요한건 마우스 포인터의 위치가 아니라 a의 끝점과 b의 끝점의 x, y 좌표가 필요하다.
그래서 이 x, y 좌표를 구하기 위해 또 삼각형을 찾아보면

이런식으로 직각삼각형을 또 그릴 수 있게 된다. (일단 θ1 + B는 설명하기 쉽게 θ1을 바꿨다)
그런데 이전에서 θ1을 구했기 때문에 a 부분의 삼각형과 b부분의 삼각형의 밑변과 높이를 구할 수 있게 된다..!
계속 말하고 있지만..
밑변을 구하는건 빗변 * cos(θ1)이고 높이는 빗변 * sin(θ1)이기 때문에 각 삼각형의 밑변 높이를 구한다면??
a의 밑변과 높이를 구할 경우 a * cos(θ1), a * sin(θ1)으로 구할 수 있고 b의 밑변과 높이를 구할 경우 어차피 쫙 펴져있는 경우에만 구하는거라서 (a + b) * cos(θ1), (a + b) * sin(θ1)으로 구할 수 있게 된다.
어쨋든 밑변은 x 높이는 y로 되기 때문에 이걸 C++로 구현해보면
float theta1 = atan2(mouse_y, mouse_x);
float x2 = (a + b) * cos(theta1);
float y2 = (a + b) * sin(theta1);이렇게 된다. x2, y2로 한 이유는 두번째 팔의 끝점을 구하는 거기 때문에.. 첫번째 팔의 끝점은 x1, y1..
이론 적용
암튼 여기에서도 계산했던 곳이 센터가 0, 0일 경우일 때 구한 것이기 때문에 각 x2, y2에 중앙으로 갈 수 있게 값을 더 해준다!
float mouse_x = point.x - center_point_xy.x;
float mouse_y = point.y - center_point_xy.y;
float theta1 = atan2(mouse_y, mouse_x);
float x2 = (a + b) * cos(theta1) + center_point_xy.x;
float y2 = (a + b) * sin(theta1) + center_point_xy.y;그럼 이렇게 되면 각 필요한 x, y좌표가 구해진다..!
이론 적용 및 코드 수정
근데 이제 여기에서 이전 글에서 한 코드에 그대로 넣으면.. 코드에서 중복 코드가 많아진다.. 그래서 그 중복 코드는 없애고 고친결과..! 이렇게 완성되었다!
void MainPage::CalIKPos(float2 point) {
float a = joint_1_line_size; // 빨간색 라인의 길이
float b = joint_2_line_size; // 파란색 라인의 길이
float c = distance(center_point_xy, point); // 첫점과 끝점을 이은 길이
// https://youtu.be/IKOGwoJ2HLk
// x2, y2는 끝점 x1, y1은 중간점 x0, y0은 센터점
// center_point_xy의 x와 y로 빼는 이유는 IK를 구현하는 곳이 250, 250인 중앙이여서 이걸 0, 0으로 옮기기 위해
float mouse_x = point.x - center_point_xy.x;
float mouse_y = point.y - center_point_xy.y;
float theta1 = 0, theta2 = 0;
float x2 = 0, y2 = 0;
// a와 b의 최대 길이는 a + b가 됨, 그리고 c는 빗변이 되고 a + b를 넘으면 안됨.. 넘으면 삼각함수로 계산이 불가함, 그렇기에 미리 맞는지 확인하는 것
if (c <= a + b) {
// IK를 구현하기 위한 각도 계산
theta2 = -acos((pow(mouse_x, 2) + pow(mouse_y, 2) - pow(a, 2) - pow(b, 2)) / (2.0 * a * b));
theta1 = atan2(mouse_y, mouse_x) - atan2(b * sin(theta2), a + b * cos(theta2));
// 위에서 theta1구할 때 theta1 + B에서 B를 뺐을 때 그 B 값을 theta1으로 사용해서 밑변과 높이를 구할 수 있긴 하지만..
// 굳이 필요 없는 계산을 해야하기도 하고.. 굳이 할 필요가 없기 때문에 그냥 마우스 포인트로 되게 함
x2 = mouse_x + center_point_xy.x;
y2 = mouse_y + center_point_xy.y;
}
else {
// 마우스 포인트와 선을 이어서 삼각형을 만들고 theta1의 각도를 얻어서
// 마우스 포인트와 선을 이은거에서 중간점은 구하는 방식이 같기 때문에 넘기고, 끝점을 구하는게 목적이기 때문에
// 끝점을 구하기 위해 쫙 폈을 때 a + b이기 때문에 그걸로 밑변과 높이를 구하는거
theta1 = atan2(mouse_y, mouse_x);
x2 = (a + b) * cos(theta1) + center_point_xy.x;
y2 = (a + b) * sin(theta1) + center_point_xy.y;
}
// 중간 점의 x와 y를 cos, sin으로 구하는 것
float x1 = a * cos(theta1) + center_point_xy.x; // x, y를 더한 이유, 위에서 x, y에 빼줬었으니 다시 더하는 것
float y1 = a * sin(theta1) + center_point_xy.y;
joint_1_point_xy = { x1, y1 };
joint_2_point_xy = { x2, y2 };
char debug[512];
sprintf_s(debug, "theta1 = %.2f, theta2 = %.2f", theta1 * 180.0 / M_PI, theta2 * 180.0 / M_PI);
debugText2().Text(to_hstring(debug));
}저기 주석에서도 말하는 것 처럼 c <= a + b가 성립이 될 때 그냥 마우스 포인터로 하는 이유는 θ1 + B를 구해서 할 순 있긴 하지만.. 이 경우 새로운 변수도 만들어야 하고.. 굳이 계산을 해서 필요없는 계산을 하게 하기 싫어서가 이유이기도 하다..
결과
그래서 이걸로 된 결과물은 이렇다!!
엄청 잘 된다!!!
2일 동안의 공부는 잘한 것 같다!
이거는.. 이전 글 쓰고.. 바로 계산해서 1시간 안에 찾고 고친걸 적고 있는건데.. 물론 간단한 식인건 맞지만.. 빠른 속도로 1시간 안에 이걸 구하고 바로 적용한게.. 2일동안 허무한 공부를 한 보람이 있는 것 같다..! 만약 그 공부가 없었다면 이걸 1시간 안에 해내지 못했을 것이다.. 왜냐면.. 공부를 하기전에는.. 라인을 그려서 유클리드 거리로.. 어떻게든 해서 두번째 x, y를 구해볼까 생각했었는데.. 지금 생각해보니.. 만약 그렇게 했다면 각도를 알 수 없어서 두번째 x, y를 전혀 구할 수 없었을 것이다.. 뭐.. 다른 방법은 있겠지만.. 내가 생각한 방법도 맞는 것 같다..!
계속 하면서 삼각형은 진짜.. 대단한 도형이라고 생각된다.. 삼각형으로 내가 필요한 대부분의 것을 구현하거나 얻을 수 있다는 것이.. 진짜 너무나도 신기하다..
암튼 까먹지 않을려고 구하고 적용하자마자 쓰다보니.. 새벽 1시 25분.. 바로 자야겠다..
암튼 끝!!
'개발 > Scara Program' 카테고리의 다른 글
| C++로 SCARA 제어 프로그램 제작하기 Pt. 4 (Inverse Kinematics 선택 제어) (0) | 2023.12.17 |
|---|---|
| C++로 SCARA 제어 프로그램 제작하기 Pt. 2-2 (Inverse Kinematics 구현하기 - 성공) (0) | 2023.12.14 |
| C++로 SCARA 제어 프로그램 제작하기 Pt. 2-1 (Inverse Kinematics 구현하기 - 실패) (0) | 2023.12.14 |
| C++로 SCARA 제어 프로그램 제작하기 Pt. 1 (WinRT 프로젝트 준비) (0) | 2023.12.13 |